LH8 - La LH vivifiante
$1, 1, 1, 2, 5, 12, 35, 108, 369, 1285, 4655, 17073, 63600, 238591...$
Que pensez-vous de cette suite ? Elle semble plutôt incongrue, non ? Et pourtant... cette suite, c'est la suite numéro 105 de l'Encyclopédie en ligne des suites de nombres entiers (en anglais On-Line Encyclopedia of Integer Sequences, OEIS), qui en contient plusieurs centaines de milliers! Mais qu'a-t-elle de si spéciale ?
Bonjour tout le monde ! Aujourd'hui j'aimerais parler d'un concept mathématique : les Polyominos.
Vous avez déjà joué à Blokus ? C'est un jeu assez sympa (et un peu un jeu de Fokus parfois, mais ne nous égarons pas) qui consiste à placer ce que l'on appelle des blocs de quatre couleurs différentes sur une grille. Ci-dessous, les blocs correspondent aux $n$-polyominos pour $n = 1$ à $5$.
On peut notamment reconnaître ces polyominos (plus précisément, des tétrominos car tous les polyominos de Tetris sont formés de $4$ blocs) dans le jeu Tetris, même si celui là fait la différence entre les blocs ci-dessous :
Dans le jeu Blokus, les joueurs peuvent tout à fait manipuler les blocs en les tournant et les retournant. On s'intéressera à ceux-là pour ne pas trop compliquer les choses. Dit autrement, les deux blocs du dessus, on considère que ce sont les mêmes !
Bref. Je me suis dit :
Tiens, et si j'essayais moi-même de coder ces blocs pour faire un jeu de Blokus mais avec des blocs à 6 carrés ? Ça ne devrait pas être compliqué, si ?
Toute cette shitstorm est partie de là... et puis...
Problème ! J'ai essayé de représenter ces blocs avec des graphes, des mots, des listes de directions... mais à chaque fois, il y avait un problème. Un p**** de problème...
Pour essayer de faire une zoologie des $n$-polyominos, on pourrait tout simplement procéder en représentant chaque bloc par une matrice, en générant toutes les matrices possibles, puis leurs symétries, puis leurs rotations... je me suis dit que c'était peut-être un peu simple, mais clairement, ce n'était pas satisfaisant. Je me suis mis en quête de la meilleure représentation possible de ces blocs. Et puis, qui sait ? Si j'arrive à trouver une structure inductive, cela pourrait énormément faciliter un futur processus de dénombrement, non ?
Une première idée serait évidemment de considérer que chaque bloc est un arbre, sur lequel on arrive à imposer une contrainte pour que chaque arbre puisse représenter un bloc, et réciproquement. On arrive immédiatement à un problème : le réciproquement est d'une part très énervant, mais la structure d'arbre seule ne suffit pas : on doit l'augmenter pour prendre en compte les différentes directions possibles, puis il faut une contrainte pour ne pas qu'un carré soit deux fois au même endroit, puis le nombre d'arbres dépasse très vite le nombre de polyominos. Bref, c'est une fausse solution...
(exemple de soucis ? carré pour $n = 5$)
Avec une liste, on pourrait penser pouvoir représenter des sortes de lignes que l'on replie sur elles-mêmes. En ajoutant des contraintes, comme par exemple, toujours commencer par un pas en avant, et faire en sorte que le premier virage soit à droite (par symétrie, sans perte de généralité, un bloc avec des virages dans un sens est semblable au même bloc en inversant les virages). Et ça semble fonctionner pour $n$ petit!... Mais évidemment, ça ne convient pas non plus... D'une part parce que pour certains blocs, il y a toujours un souci de représentations multiples pour un même bloc, mais aussi tout simplement un problème de carrefours ! Le bloc Tetris ne peut pas être représenté par un mot de longueur $4$... il faut revenir sur ses pas pour gérer l'embranchement...
Voilà
Fort de cela, je n'admet pas j'admets ma défaite. Je me mets donc à rechercher le problème... et je tombe sur l'article Wikipédia sur le sujet...
Un article assez complet, qui évoque clairement le problème du dénombrement, et les différentes méthodes utilisées pour faire la zoologie de ces polyominos. Et là, c'est la douche froide.
Bon, maintenant on sort de la douche, on est tout propre, on se sèche, puis on se détend. Compter les polyominos, c'est pas simple. Mais ces polyominos peuvent avoir des propriétés très intéressantes pour les amateur·ices de mathématiques récréatives.
Bon, je met ça dans une sous-section topo parce qu'il y a des trous mais bon, ça pourrait aussi être la section Télétouze
À partir de $n = 7$, on est en mesure de trouver des polyominos à trous ! Suite 1 419...
On considère qu'il y a un trou dès lors qu'un carré vide est entouré de $4$ carrés pleins, sans compter ceux qui n'ont une intersection qu'aux sommets (et non pas de 8 carrés pleins).
Autre chose hyperintéressante, on a conjecturé que :
$$ \frac{\text{nombre de } n \text{-polyominos avec des trous}}{\text{nombre de } n \text{-polyominos tout court}} \underset{n \rightarrow +\infty}{\longrightarrow} 1 $$
Et oui! Plus $n$ augmente, plus le ratio de polyominos à trous semble augmenter... ce qui est un peu triste, parce qu'une personne imaginaire qui essaie de jouer à Blokus ou a Tetris avec des polyominos troués a clairement eu zéro sur vingt.
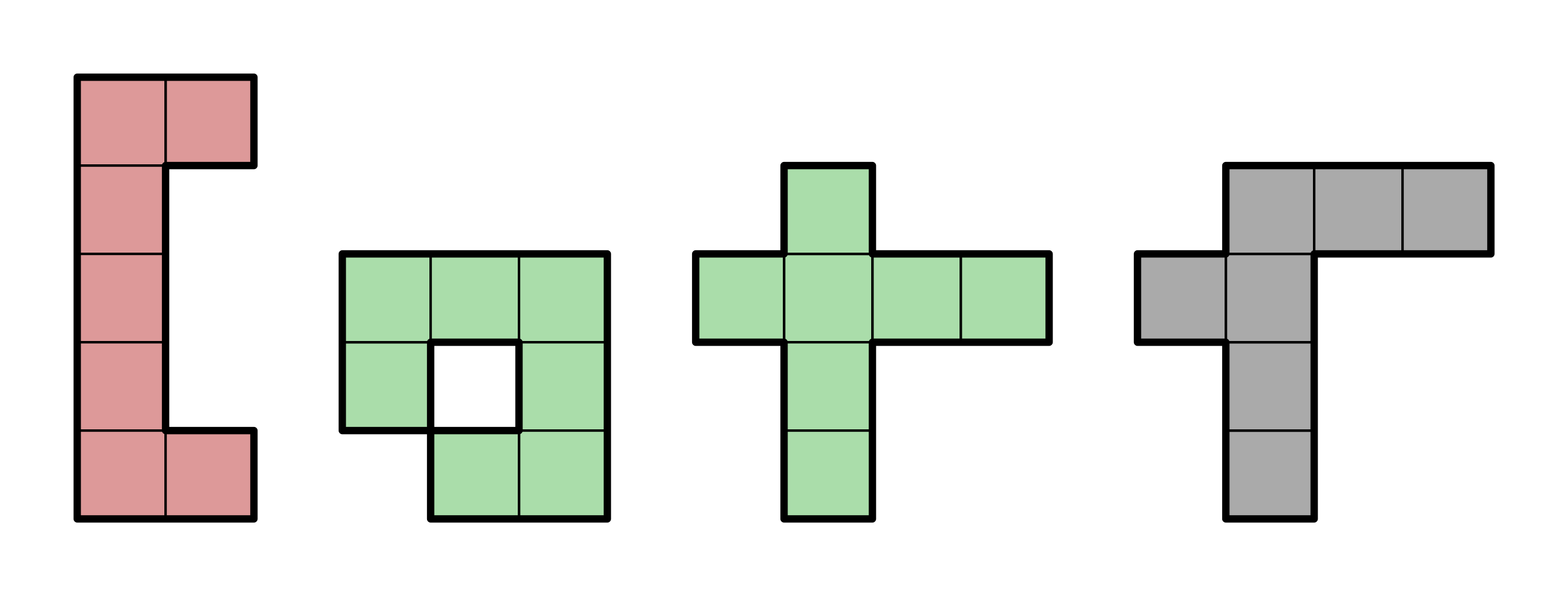
On a pu déterminer de manière rigoureuse une évolution asymptotique du nombre de $n$-polyominos :
$$ \lim_{n \rightarrow +\infty} (\text{nombre de }n\text{-polyominos})^{\frac{1}{n}} = \lambda $$
avec $\lambda$ de l'ordre de $4$ ou $4,5$. C'est massif.
Oui, oui, je vous entends. Les polyominos, c'est pas si fou que ça en fait. Pourquoi ?
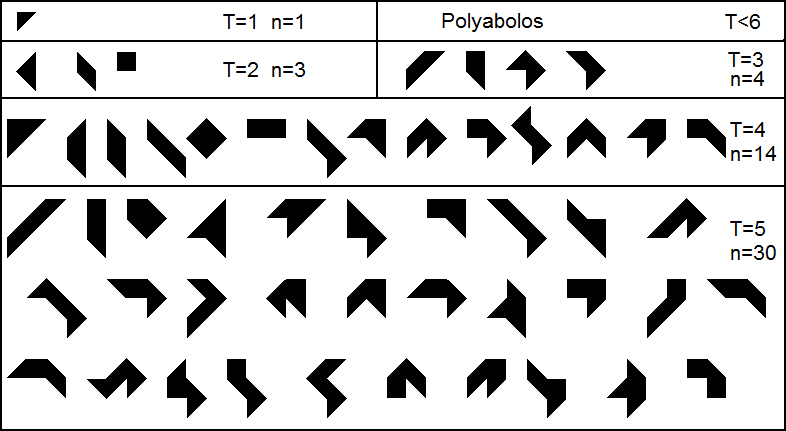
Et bien il y a les polyabolos! Ce sont des assemblages de triangles isocèles rectangles. Leur nombres constituent la suite 6 074 de l'OEIS.
Oh, mais il y a aussi les polyiamonds, c'est la même chose mais avec des triangles équilatéraux. Suite 577
Ou les polydrafters. Des triangles dont les angles valent respectivement $30°$, $60°$ et $90°$... Suite 56 842...
Roh, et puis si vous préférez les hexagones... Intéressez-vous aux polyhexs! Les travaux sur ces curiosités géométriques trouvent des application en chimie! Suite 228
Hexagons are the bestagons
Vous préférez les segments ? Pas de problème ! Jetez donc un œil aux polysticks!
Vous voulez faire passer vos carrés en dimension $3$ ? Les polyominoïdes sont fait pour vous!
La dimension $2$ vous semble insipide ? Mais passez-donc aux polycubes!
Et puis les polyhypercubes!
Et puis! Et puis... et puis...
Épuisé. Je suis épuisé. J'ai écrit un tiers de PACE sur les polyominos. Il est 2 heures du matin... et puis bon, si vous voulez inventer une nouvelle polyforme indénombrable en dimension 79, libre à vous, hein ? Mais vous n'en verrez jamais le bout :)
